Abstract
There are various metrics and indices that track the health and performance of the U.S. Securities market. While some track sectors such as technology (NASDAQ), others track a portion of top-performing companies (S&P 500). This article walks through the relationship between the returns of a company (Apple) and those of the general markets. We discuss the implications of this market-based returns model and attempt to contextualize its residuals. We conclude that certain highly significant residuals--unjustified by company news/corporate events--may contain profit opportunities. If anything, their distribution could provide insight into the market efficiency of a company across time.
Hypothesizing a Market Relationship
We hypothesize that the performance of any company is invariably tied--to some degree--to the general securities market. Why would this be the case? Let's consider the example of Apple Inc. Apple's market return is largely dependent on its ability to turn a profit selling its products. The ability to profitably produce these products (iPhone, iPad, Mac, etc.) depends on many interactions with the general market. Fluctuations in industries producing glass, aluminum, skilled labor, software, silicon, battery-grade lithium, and manufacturing tools would all affect this ability. Further, changes in consumer confidence, interest rates, and demand in the equities markets affect the market as a whole, including Apple.
Visualizing a Market Relationship
These fluctuations and changes are visible in the metrics and indices described above. To illustrate this, we collected adjusted close data for Apple (AAPL) and an S&P 500 ETF (SPY) [1] from Jan 2019 - Jul 2022. All further plots and statistics in this article are derived from this data. To begin the analysis, we observe a scatterplot between SPY log returns (x-axis) and AAPL log returns (y-axis).
Figure 1: Natural log-transformed returns for AAPL and SPY (Jan 2019 - Jul 2022)

There is a visible linear association. A linear regression model [ ln(1+AAPL) = 1.228 * ln(1+SPY) + 0.00862 ] explains about 65% (Adj. R^2) of the variation in AAPL returns. We see that the model is not perfect, which is expected. The remaining variability in Apple returns (~ 35%) is a result of its unique business decisions and operational efficiency.
We also observe the model-fitted values over time to gain a more comprehensive view of the model's variation features and performance. Figure 2 plots model-predicted returns to actual AAPL returns (log-transformed).
Figure 2: Natural log-transformed AAPL returns and model-fitted values (Jan 2019 - Jul 2022)
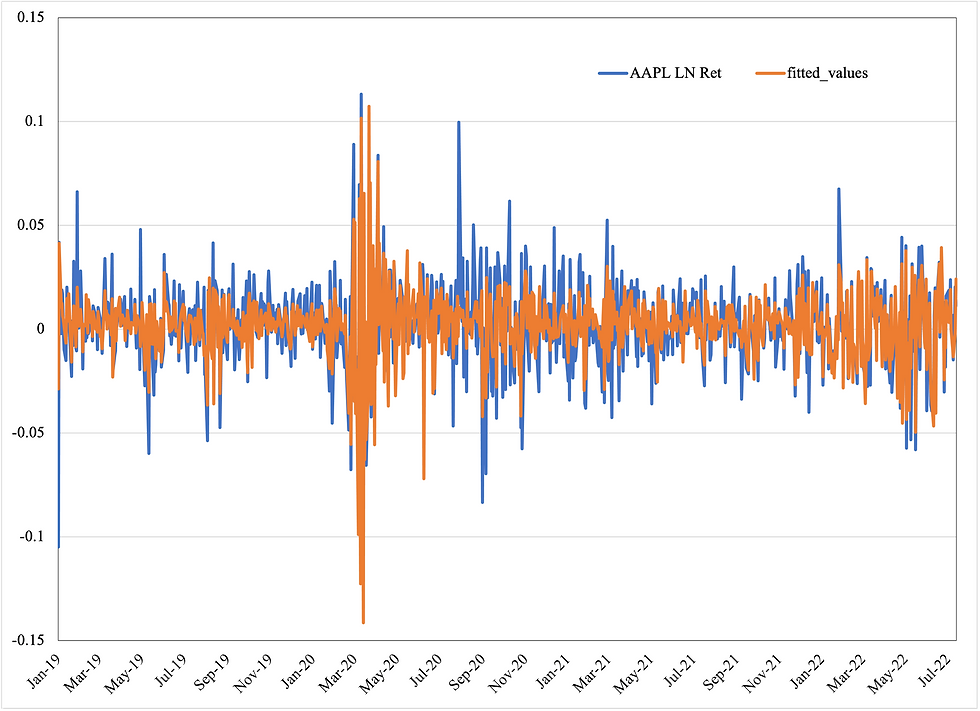
From Figure 2, we visualize the predictive power of our market-based returns model. The residuals (errors) of the model are also visible. These residuals represent days where AAPL either outperformed or underperformed the reasonable market-based prediction. Hence, we interpret them as market-independent returns.
Quantifying Model Residuals
To contextualize the residuals, we create a standardized t-statistic [see code] (Student's t distribution) to measure the statistical significance of each residual. Then, we highlight the top 5% of these residuals, (t > 1.65) and look into any contextual evidence.
Figure 3: Residual t-statistics of AAPL log-transformed returns with highlighted days (Jan 2019 - Jul 2022)

Contextualizing Model Residuals
Nearly all of the highlighted days in Figure 3 appear as neatly placed peaks in the time series. Logically, there is a natural question about what happened during those days. Surely, on a day where Apple largely outperforms the market-based expectation, we would expect some context. Out of 42 highlighted days, 19 days involve an earnings release, stock split, product launch, or major conference/keynote. The remaining 23 days have little to no associated news as far as we know.
The 19 days with associated context describe the significance of those residuals, however, the 23 other days remain with little historical context. The most logical explanation for most of these points could be the natural investor demand edge Apple enjoys over the general market. It is, in fact, the largest (market cap) publically traded company in the world. Apple also contains a strong demand from large institutional investors, which has only increased during this observed period [2]. Investors could be buying into shares during times the general market provides a lackluster return or future expectation.
Potential Profits from Market Corrections
However, there is one more possible explanation. We hypothesize that there could be days where a statistically significant market outperformance is not justified by business-relevant news or any signs of increased + sustainable equity demand. On those days, the company's stock price could be slightly mispriced and we could exploit this opportunity. Figure 4 shows adjusted close prices for AAPL during the observed period marked with the highlighted days.
Figure 4: AAPL Adjusted Close Prices marked by Highlighted Days (Jan 2019 - Jul 2022)

Suppose we take a 1-day long short position on each of the highlighted peaks. Would we find enough instances for a profit? What if we take a 2-day short position at each point? Should we include points with earnings and/or significant news? Table 1 considers the results of this approach in different cases.
Table 1: Profit from a k-day short position
| All points | Non-News Points Only |
k = 1 | $7.88 | $13.92 |
k = 2 | $30.97 | $15.76 |
From Table 1, we observe a small positive edge in all cases. We also notice that considering all highlighted points into the strategy is expectedly volatile across k. It includes large losses and gains from volatile events such as earnings, splits, product launches, and notable press releases. All of these events are invariably material to investors. However, we observe that when we exclude these extreme events, the total profits (Table 1) become much less variable across the board. It is unwise to consider a k greater than 2 since the strategy could be separated from the mispriced event it hopes to capture and instead be more sensitive to trends.
Conclusions and Implications
In this article, we examine the relationship between a company (Apple) and the general securities market. We base this relationship on the hypothesis that every company's ability to produce profit is somewhat rooted in the health of the general market. We create a linear returns model for Apple from (Jan 2019 - Jul 2022) and observe the behavior of statistically significant residuals.
In a relatively small sample size (n = 890 days), we observed that there were points where large market outperformance was unsustainable. By taking a k-day short position (excluding volatile business events), we observed a small positive edge. However, there is an implication to take into account. First and foremost, all companies come with varying degrees of market efficiency. Apple would very reasonably be on top of that list, making it challenging to accurately point to mispriced days without substantial evidence. However, by carefully implementing the improvements below and studying smaller, less efficient companies, we would be heading in the right direction.
At the very least, we would gain a better understanding of the distribution of these significant residuals across companies with varying degrees of liquidity and market efficiency.
Improving Independent Variables
In our experiment, we used the SPY ETF as an independent variable representing changes in the general market. Any ETF is somewhat actively managed, introducing potentially artificial price changes and complications. A future study would incorporate a non-ETF market metric.
We also could consider the idea of including a metric to account for any industry effects. Industry effects would specifically impact certain companies and its impact is important to consider. The challenge here is finding a metric that is reasonably independent of the general market metric. Collinearity between independent variables [3] is logically problematic when interpreting the significance of the model and its residuals.
Improving Sampling
Improving the sample size of the training data set would certainly improve the reliability of the results. Next, applying this methodology in out-of-sample testing would further qualify the discussed methods. Since part of the methodology requires researching the business events around a certain day, considering large sample sizes could be manually intensive.
No Leverage Drawback
When applying a 1-day short position on days with no significant business news, we obtained an edge of < 10% per share shorted. Considering the sample size and variation of each profit day, the edge is likely not very large. This seems sensible considering which company we used as our example. This lends the question of any existing leverage opportunities. We hypothesize that the larger more liquid companies might have the profit from the highlighted days priced into their leveraged derivatives.
However, this isn't a definitive statement. There could exist companies where the edge could be consistently multiplied through leveraged instruments. In that case, you have found your gold.
Improving Diversification
It would be logical to use this model in conjunction with other technical and foundational factors to build your edge. These models are traditionally used in the analysis of business significant events from an objective point of view. However, it is reasonable to claim that if such a model were combined sensibly with other counterparts, we could expect a sustainable and well-sized edge, if one exists for the company.
Citations + Code
[2] https://fintel.io/so/us/aapl
[3] https://statisticsbyjim.com/regression/multicollinearity-in-regression-analysis/
[Code]
import yfinance as yf
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import math
import openpyxl
# Beta-Based Residuals Analysis #####################################
# Model is based of Natural Log Returns
xtick, ytick = "SPY", "AAPL"
data = yf.download("{} {}".format(xtick, ytick), start = "2019-01-01")
# Returns for Tickers: date is one day forward
x = np.array(data[('Adj Close', xtick)].pct_change()[1:])
y = np.array(data[('Adj Close', ytick)].pct_change()[1:])
# Natural Log Returns
lnx = np.log(1+x)
lny = np.log(1+y)
xcopy = lnx.reshape(-1,1)
model = LinearRegression().fit(xcopy, lny)
a, b = model.coef_[0], model.intercept_
# Fitted Values
fitted_values = model.predict(xcopy)
# Residuals
resid = lny - fitted_values
# t-stat of residuals
assert len(resid) == len(x)
rse = math.sqrt(sum(resid**2) / (len(x) - 2))
t = resid / rse
# Summary Stats
print("ln({}) = {}*ln({}) + {}".format(ytick, a, xtick, b))
print("R^2: {}".format(model.score(xcopy,lny)))
print("SS Residuals: {}".format(sum(resid**2)))
# Plot fitted Values with Actual Y-axis
plt.plot(lny, 'b')
plt.plot(fitted_values, 'r')
plt.title("Training Set")
plt.show()
# Plot peaks based on t-stat limit
# Is a peak if: t-stat is above limit and return is positive
tlim = 1.65
closes = np.array(data[('Adj Close', ytick)][1:])
assert len(closes) == len(t)
cpeaks = [closes[i] if t[i] > tlim and y[i] > 0 else float('nan') for i in range(len(t))]
# Perfect Peaks
perfect_peaks = [closes[i] if y[i+1] < 0 < y[i] else float('nan') for i in range(len(y)-1)]
perfect_peaks.append(float('nan'))
plt.plot(closes)
plt.plot(cpeaks, '.')
plt.show()
# Plot t-stat across time with peaks
tlim = 1.65
assert len(t) == len(y)
tpeaks = [t[i] if t[i] > tlim and y[i] > 0 else float('nan') for i in range(len(t))]
plt.plot(t)
plt.plot(tpeaks, '.')
plt.show()
# Build CSV Worksheet
assert len(data.index[1:]) == len(t)
d = [data.index[1:], np.array(data[('Adj Close', xtick)][1:]), np.array(data[('Adj Close', ytick)][1:]), x, y, lnx, lny, fitted_values, resid, t]
col = ['Date', '{} Adj Close'.format(xtick), '{} Adj Close'.format(ytick), "{} Ret".format(xtick), "{} Ret".format(ytick), "{} LN Ret".format(xtick), "{} LN Ret".format(ytick), "fitted_values", "Residuals", "Tstat"]
df = pd.DataFrame()
for x, y in zip(d, col): df[y] = x
df.to_csv("test1.csv", index = False)
#DONE##############################################################################